edu-fp

# Разное

## Интересный пример необоснованной рекурсии

Гипотеза Коллатца: функция вида f(n)=(n/2,^n=0; 3*n+1,^n=1) всегда достигает 1.
Одна из нерешённых проблем математики.

```text
collatz :: Int -> Int
collatz 1 = 1
collatz n =
  if (even n)
    then (n `div` 2)
    else (3 * n + 1)
```

Самое удивительное в том, что мы придём к такому результату, с какого бы числа мы ни начали.

----

![](figures/collatz.jpg)

Так как гипотеза не доказана для всех чисел, то, хоть она и выполняется за конечное время для большинства проверенных чисел, это не означает, что она будет выполняться всегда (то есть может существовать число, при котором рекурсия будет бесконечной)

---

## Functors

### Value as is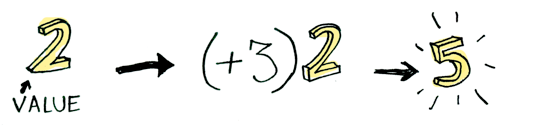

![](figures/monad-value.png)
![](figures/monad-value-apply.png)

![](figures/monad-value-and-context.png)

Source: [Functors, Applicatives, And Monads In Pictures](https://adit.io/posts/2013-04-17-functors,_applicatives,_and_monads_in_pictures.html)

----

### Maybe

```haskell
data Maybe a = Nothing | Just a
```

![](f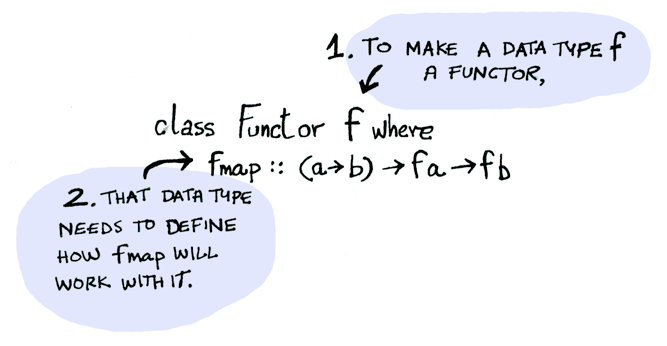igures/monad-context.png)
![](figures/monad-no-fmap-ouch.png)

----

### Functor

![](figures/functor-def.png)

![](figures/fmap-def.png)

----

### Maybe as a Functor

```haskell
instance Functor Maybe where
    fmap func (Just val) = Just (func val)
    fmap func Nothing = Nothing
```

#### Fmap for Just a Value

![](figures/fmap-just.png)

</div><div class="col">

#### Fmap for Nothing

![](figures/fmap-nothing.png)

</div></div>

----

#### Fmap for a List

![](figures/fmap-list.png)

---

## Monad as `andThen`

![](figures/monad-tutorial.jpeg)

Много материалов заимствовано тут: [Haskell Beginners 2022 — Lecture 4: Monads and IO — Dmitrii Kovanikov](https://slides.com/haskellbeginners2022/lecture-4)

----

### Maybe, yes? Maybe, no?

```haskell
data Maybe a = Nothing | Just a
```

Жуткий типичный код:

```haskell
maybePlus :: Maybe Int -> Maybe Int -> Maybe Int
maybePlus ma mb = case ma of
    Nothing -> Nothing
    Just a  -> case mb of
        Nothing -> Nothing
        Just b  -> Just (a + b)
```

Типичная функция-подпорка:

```haskell
andThen :: Maybe Int -> (Int -> Maybe Int) -> Maybe Int
andThen ma f = case ma of
    Nothing -> Nothing
    Just x  -> f x
```

Рефакторинг:

```haskell
maybePlus :: Maybe Int -> Maybe Int -> Maybe Int
maybePlus ma mb = andThen ma (\a -> andThen mb (\b -> Just (a + b)))
```

----

### Either way

```haskell
data Either a b = Left a | Right a
```

Жуткий типичный код:

```haskell
eitherPlus :: Either String Int -> Either String Int -> Either String Int
eitherPlus ea eb = case ea of
    Left err -> Left err
    Right a  -> case eb of
        Left err -> Left err
        Right b  -> Right (a + b)
```

Типичная функция-подпорка:

```haskell
andThen :: Either e a
        -> (a -> Either e b)
        -> Either e b
andThen ea f = case ea of
    Left err -> Left err
    Right x  -> f x
```

Рефакторинг:

```haskell
eitherPlus :: Either String Int -> Either String Int -> Either String Int
eitherPlus ea eb = andThen ea (\a -> andThen eb (\b -> Right (a + b)))
```

----

### Multiple combinations

Жуткий типичный код:

```haskell
listPlus :: [Int] -> [Int] -> [Int]
listPlus la lb = case la of
    []     -> []
    a : as -> case lb of
        [] -> []
        bs -> map (+ a) bs ++ listPlus as bs
```

Что делает? `listPlus [1,2] [3,4] => [4,5,5,6]`

Типичная функция-подпорка:

```haskell
andThen :: [Int] -> (Int -> [Int]) -> [Int]
andThen l f = case l of
    []     -> []
    x : xs -> f x ++ andThen xs f
```

Рефакторинг:

```haskell
listPlus :: [Int] -> [Int] -> [Int]
listPlus la lb = andThen la (\a -> andThen lb (\b -> [a + b]))
```

----

### Is there a pattern?

```haskell
andThen :: Maybe    a  -> (a -> Maybe    b)  -> Maybe    b
andThen :: Either e a  -> (a -> Either e b)  -> Either e b
andThen ::         [a] -> (a ->         [b]) ->         [b]
```

```haskell
maybePlus  ma mb = andThen ma (\a -> andThen mb (\b -> Just  (a + b)))
eitherPlus ea eb = andThen ea (\a -> andThen eb (\b -> Right (a + b)))
listPlus   la lb = andThen la (\a -> andThen lb (\b ->       [a + b]))
```

How to generalize?

<div>

- Polymorphic andThen
- Polymorphic constructor

</div>

---

## Monad

```haskell
class Monad m where
    return :: a -> m a
    (>>=)  :: m a -> (a -> m b) -> m b
```

- What we can already learn from the definition?
    - Monad is a typeclass
    - It has two methods
    - The second method is an operator (it's called bind)
    - It's a typeclass for type constructors like Maybe and not, e.g., Int
- What we can't see from the above?
    - Instances implementations
    - Laws
    - How to use this abstraction efficiently
    - Why it's called Monad

----

### Instances

```haskell
class Monad m where
    return :: a -> m a
    (>>=)  :: m a -> (a -> m b) -> m b
```

```haskell
instance Monad Maybe where
    return :: a -> Maybe a
    return x = Just x

(>>=) :: Maybe a
          -> (a -> Maybe b)
          -> Maybe b
    Nothing >>= _ = Nothing
    Just x  >>= f = f x
```

</div><div class="col">

```haskell
instance Monad (Either e) where
    return :: a -> Either e a
    return x = Right x

(>>=) :: Either e a
          -> (a -> Either e b)
          -> Either e b
    Left e  >>= _ = Left e
    Right x >>= f = f x
```

</div></div>

```haskell
instance Monad [] where
    return :: a -> [a]
    return x = [x]

(>>=) :: [a] -> (a -> [b]) -> [b]
    l >>= f = concatMap f l
```

----

### Laws

```haskell
instance Monad Maybe where
    return :: a -> Maybe a
    return x = Just x
    ...
```

</div><div class="col">

```haskell
instance Monad Maybe where
    return :: a -> Maybe a
    return x = Nothing
    ...
```

</div></div>

1. Left identity: `return a >>= f === f a`
1. Right identity: `m >>= return === m`
1. Associativity: `(m >>= f) >>= g === m >>= (\x -> f x  >>= g)`

----

### Refactoring 1/2

```haskell
maybePlus :: Maybe Int -> Maybe Int -> Maybe Int
maybePlus ma mb = andThen ma (\a -> andThen mb (\b -> Just (a + b)))
```

Запишем в инфиксном стиле:

```haskell
maybePlus :: Maybe Int -> Maybe Int -> Maybe Int
maybePlus ma mb = ma `andThen` (\a -> mb `andThen` (\b -> Just (a + b)))
```

Уберём лишние скобки:

```haskell
maybePlus :: Maybe Int -> Maybe Int -> Maybe Int
maybePlus ma mb = ma `andThen` \a -> mb `andThen` \b -> Just (a + b)
```

Заменим `andThen` на `>>=`

```haskell
maybePlus :: Maybe Int -> Maybe Int -> Maybe Int
maybePlus ma mb = ma >>= \a -> mb >>= \b -> return (a + b)
```

----

### Refactoring 2/2

```haskell
maybePlus :: Maybe Int -> Maybe Int -> Maybe Int
maybePlus ma mb = ma >>= \a -> mb >>= \b -> return (a + b)
```

Обобщим

```haskell
monadPlus :: Monad m => m Int -> m Int -> m Int
monadPlus ma mb = ma >>= \a -> mb >>= \b -> return (a + b)
```

Перепишем с синтаксическим сахаром `do` нотации.

```haskell
monadPlus :: Monad m => m Int -> m Int -> m Int
monadPlus ma mb = do
  a <- ma
  b <- mb
  return (a + b)
```

---

## Monad as a Context

```python
class GraphBuilder():

def addNode(self, name):
    assert checkNode(self, name), "err"
    self.nodes.append(name)

def connect(self, a, b):
    assert checkEdge(self, a, b), "err"
    self.edges.append((a, b))

def initialNodes(self): ...
  def render(self): ...
```

</div><div class="col">

```haskell
data Graph = Graph
  { nodes :: [Node]
  , edges :: [(String, String)] }

addNode name g@Graph{ nodes=nodes }
  | not (checkNode name g)
  = error "err"
  | otherwise
  = g{ nodes=name : nodes }

connect a b g@Graph{ edges=edges }
  | not (checkEdge a b g)
  = error "err"
  | otherwise
  = g{ edges=(a, b) : edges }

initialNodes Graph{  } = ...
render Graph{...} = ...
```

</div></div>

----

```python
g = GraphBuilder()
g.addNode("a")
g.addNode("b")
g.addNode("c")
g.connect("a", "b")
g.connect("b", "c")

nodes = g.initialNodes()
g.addNode("0")
for n in nodes:
    g.connect("0", n)
```

</div><div class="col">

```haskell
g1 = connect "b" "c"
  $ connect "a" "b"
    $ addNode "c"
      $ addNode "b"
        $ addNode "a"
          $ Graph [] []

nodes = intialNodes g1
g2 = addNode "0" g1
g3 = foldl
       (\g n -> connect "0" n g)
       g2 nodes
```

```haskell
g1 = foldl (\st f -> f st) (Graph [] [])
    [ addNode "a"
    , addNode "b"
    , addNode "c"
    , connect "a" "b"
    , connect "b" "c"
    ]
```

</div></div>

----

### State

Взято тут: [DERIVING THE STATE MONAD FROM FIRST PRINCIPLES](https://williamyaoh.com/posts/2020-07-12-deriving-state-monad.html)
(вернее её упрощённая версия)

```haskell
newtype State s a = State { runState :: s -> (s, a) }
```

![](figures/monads-state-data.png)

----

#### State Monad

```haskell
instance Monad (State s) where
  return = pure
  State stateX >>= nextFn = State $ \s ->
    let (s', x) = stateX s
     in runState (nextFn x) s')
```

![](figures/monads-state-bind.png)

----

#### State Monad Get/Set/Modify

```haskell
get :: State s s
get = State (\s -> (s, s))

put :: s -> State s ()
put s = State (\_ -> (s, ()))

modify :: (s -> s) -> State s ()
modify f = get >>= (\s -> put (f s))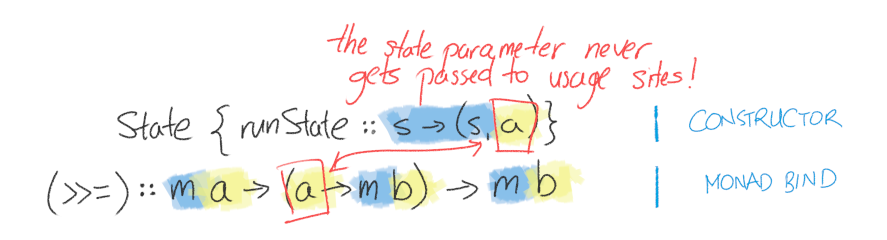
```

![](figures/monads-state-get.png)

----

#### State Functors

```haskell
instance Functor (State s) where
  fmap f (State stateFn) = State (\s ->
    let (s', result) = stateFn s
    in (s', f result))

instance Applicative (State s) where
  pure x = State (\s -> (s, x))
  (State stateFx) <*> (State stateX) = State (\s ->
    let (s', fx) = stateFx s
        (s'', x) = stateX s'
     in (s'', fx x))
```

----

#### Back to Graph Builder

```haskell
addNode name = do
    g@Graph{ nodes=nodes } <- get
    if checkNode name g
    then put g{ nodes=name : nodes }
    else error "err"

connect a b = do
    g@Graph{ edges=edges } <- get
    if checkEdge a b g
    then put g{ edges=(a, b) : edges }
    else error "err"

initialNodes = do
    nodes <- ...
    return nodes

render Graph{...} = ...

buildGraph bld = (runState bld) (Graph [] [])
```

```haskell
render $ buildGraph $ do
    addNode "a"
    addNode "b"
    addNode "c"
    connect "a" "b"
    connect "b" "c"
    nodes <- intialNodes g1
    addNode "0" g1
    mapM_ (\n -> connect "0" n) nodes
```